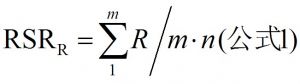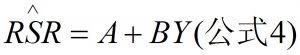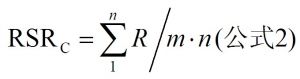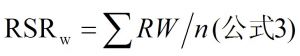秩和比法

秩和比法（Rank-sum ratio，简称RSR法），是我国学者田凤调于1988年提出的[1]，集古典参数估计与近代非参数统计各自优点于一体的统计分析方法，它不仅适用于四格表资料的综合评价，也适用于行×列表资料的综合评价。其中，秩和比(Rank-sum ratio，RSR)指的是表中行(或列)秩次的平均值，是一个非参数计量，具有0～1区间连续变量的特征。其基本思想是在一个n行(n评价对象)m列(m个评价指标)矩阵中，通过秩转换，获得无量纲的统计量RSR，以RSR值对评价对象的优劣进行排序或分档排序。 　　该法经过二十余年的发展，在广大学者的共同支持和努力下，此法已日渐完善，广泛地应用于医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面。 　　秩和比（Rank-sum ratio，RSR）法，它是一组全新的统计信息分析方法，是数量方法中一种广谱的方法，针对性强，操作简便，使用效果明显。非常适合于医学背景的广大用户。本法从理论上讲，融古典的参数统计与近代的非参数统计于一体，兼及描述性与推断性。 公卫百科

 

秩和比的计算公式 公卫论坛

秩和比(Rank-sum ratio，RSR)．它是一个内涵极为丰富的统计量，表明不同计量单位多个指标的综合水平。 　　 公卫论坛

秩和比的计算常需按行(R)或按列(C)分别进行计算： 公卫百科

公式1或公式2，式中m为指标数，n为分组数。 　　

公卫考场

几个RSR的合并方法：各组RSR→R→合并RSR。 　　

加权秩和比(RSRw)：公式3，式中w 为权重系数。 公卫百科

 

秩和比法的一般步骤

秩和比法乃指利用RSR进行统计分析的一组方法。在一个n行m列矩阵中，通过秩代换，获得无量纲统计量RSR；在此基础上，运用参数分析的概念与方法，解决综合评价、鉴别分类、因素与关联分析、统计监控、预测与决策等问题，为卫生管理和医学科技的发展服务。 　　实践表明，本法是一种涵义自明、容易推广的有效统计分析方法；本法的理论意义是再次印证了近代的非参数统计与古典的参数统计的互补作用和融合的必然性。 　　 公卫论坛

秩和比法的一般步骤 　　 公卫人

1．计算RSR； 　　 公卫考场

2．确定RSR的分布：RSR→f，f↓，秩次范围R，平均秩次，向下累计频率→Y(概率单位)； 　　 公卫考场

3．计算回归方程：如图公式4；必要时对RSR还可选用适当代换量，以达到偏态对称化的目的； 　　

4．按合理分档和最佳分档原则进行分档 公卫考场

 

  公卫论坛

秩和比法的创始人-田凤调 公卫论坛

中国预防医学科学院研究员，中国卫生统计学会顾问组长、中国卫生统计杂志副主编。曾任中华医学会卫生统计学组副组长、中国卫生统计学会副会长兼秘书长。1993年获国务院有突出贡献的科技者称号。 　　五十多年来从事卫生统计科学研究与教学工作，在普及统计信息知识和推动学术交流中作出了很大贡献。所创立的“秩和比法”是一种全新的实用数量方法，集参数统计与非参数统计于一身，有描述有推断，能提高统计分析与再分析的水平，满足人们在统计研究与统计管理中的各种需求，这是医学统计方法的创新。主编了《卫生统计应用丛书》、《医学正常值的统计研究方法》、《实用卫生统计学》、《秩和比法及其应用》等书，发表学术论文数百篇。 公卫论坛

秩和比法的优点 公卫家园

1．秩和比是一个新的统计量，是复合信息的载体，容量大，可塑性强。 　　

公卫家园

2．秩和比法是一种全新的广谱的实用数量方法，或称统计信息方法，集参数统计与非参数统计于一身，有描述、有推断，能提高统计分析与再分析的水平，满足人们在统计研究与统计管理中的种种需求，因此，我们说秩和比法是数量方法的创新，有着极为宽广的发展前景。 　　

公卫家园

3．秩和比法的关键步骤是秩代换，具有强大的统计信息功能，针对性强，柔韧性大，操作简便，应用价值高。 　　 公卫家园

4．通过移植、嫁接。利用求得的秩和比值，可以四通八达。本法在量化研究中占有重要位置，粗中有细，细中有粗，相互对照。规律、特征自然明．是做比较，找关系的有效手段。
公卫人

 

公卫人