t检验
检验
t检验分为单总体检验和双总体检验。
单总体t检验时检验一个样本平均数与一个已知的总体平均数的差异是否显著。当总体分布是正态分布,如总体标准差未知且样本容量小于30,那么样本平均数与总体平均数的离差统计量呈t分布。
单总体t检验统计量为:
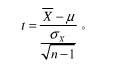
公卫人

公卫百科
双总体t检验是检验两个样本平均数与其各自所代表的总体的差异是否显著。双总体t检验又分为两种情况,一是独立样本t检验,一是配对样本t检验。
独立样本t检验统计量为:

公卫人
S1 和 S2 为两样本方差;n1 和n2 为两样本容量。(上面的公式是1/n1 + 1/n2 不是减!)
配对样本t检验统计量为:


公卫人
t检验的适用条件
(1) 已知一个总体均数;
(2) 可得到一个样本均数及该样本标准差;
(3) 样本来自正态或近似正态总体。
t检验步骤
以单总体t检验为例说明:
问题:难产儿出生体重n=35, X拔=3.42,S =0.40,一般婴儿出生体重μ0=3.30(大规模调查获得),问相同否?
解:1.建立假设、确定检验水准α
H0:μ = μ0 (无效假设,null hypothesis)
H1:μ ≠ μ0(备择假设,alternative hypothesis,)
双侧检验,检验水准:α=0.05
2.计算检验统计量
公卫论坛
3.查相应界值表,确定P值,下结论
查附表1,t0.05 / 2.34 = 2.032,t < t0.05 / 2.34,P
>0.05,按α=0.05水准,不拒绝H0,两者的差别无统计学意义

公卫百科
t检验的来历
当总体呈正态分布,如果总体标准差未知,而且样本容量 <30,那么这时一切可能的样本平均数与总体平均数的离差统计量呈
分布。
检验是用 分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。 检验分为单总体 检验和双总体 检验。
1.单总体 检验
单总体 检验是检验一个样本平均数与一已知的总体平均数的差异是否显著。当总体分布是正态分布,如总体标准差 未知且样本容量
<30,那么样本平均数与总体平均数的离差统计量呈 分布。检验统计量为:
。
如果样本是属于大样本( >30)也可写成:
。
在这里, 为样本平均数与总体平均数的离差统计量;
为样本平均数;
为总体平均数;
为样本标准差;
为样本容量。
例:某校二年级学生期中英语考试成绩,其平均分数为73分,标准差为17分,期末考试后,随机抽取20人的英语成绩,其平均分数为79.2分。问二年级学生的英语成绩是否有显著性进步?
检验步骤如下:
第一步 建立原假设 =73
第二步 计算 值
第三步 判断
因为,以0.05为显著性水平, ,查 值表,临界值 ,而样本离差的
1.63小与临界值2.093。所以,接受原假设,即进步不显著。
2.双总体 检验
双总体 检验是检验两个样本平均数与其各自所代表的总体的差异是否显著。双总体
检验又分为两种情况,一是相关样本平均数差异的显著性检验,用于检验匹配而成的两组被试获得的数据或同组被试在不同条件下所获得的数据的差异性,这两种情况组成的样本即为相关样本。二是独立样本平均数的显著性检验。各实验处理组之间毫无相关存在,即为独立样本。该检验用于检验两组非相关样本被试所获得的数据的差异性。
现以相关检验为例,说明检验方法。因为独立样本平均数差异的显著性检验完全类似,只不过 。
相关样本的 检验公式为:
。
在这里, , 分别为两样本平均数;
, 分别为两样本方差;
为相关样本的相关系数。
例:在小学三年级学生中随机抽取10名学生,在学期初和学期末分别进行了两次推理能力测验,成绩分别为79.5和72分,标准差分别为9.124,9.940。问两次测验成绩是否有显著地差异?
检验步骤为:
第一步 建立原假设 =
第二步 计算 值
=
=3.459。
第三步 判断
根据自由度 ,查 值表 , 。由于实际计算出来的 =3.495>3.250= ,则 ,故拒绝原假设。
结论为:两次测验成绩有及其显著地差异。
由以上可以看出,对平均数差异显著性检验比较复杂,究竟使用 检验还是使用 检验必须根据具体情况而定,为了便于掌握各种情况下的
检验或 检验,我们用以下一览表图示加以说明。
已知时,用
单总体
未知时,用
在这里, 表示总体标准差的估计量,它与样本标准差 的关系是:
, 已知且是独立样本时,用
是独立大样本时,用
双总体
, 未知
是独立小样本时,用
是相关样本时,用
以上对平均数差异的显著性检验的理论前提是假设两个总体的方差是相同的,至少没有显著性差异。对两个总体的方差是否有显著性差异所进行的检验称为方差齐性检验,即必须进行
检验。
编辑本段注意事项
1、选用的检验方法必须符合其适用条件(注意:t检验的前提是资料服从正态分布)
。理论上,即使样本量很小时,也可以进行t检验。(如样本量为10,一些学者声称甚至更小的样本也行),只要每组中变量呈正态分布,两组方差不会明显不同。如上所述,可以通过观察数据的分布或进行正态性检验估计数据的正态假设。方差齐性的假设可进行F检验,或进行更有效的Levene's检验。如果不满足这些条件,只好使用非参数检验代替t检验进行两组间均值的比较。
2、区分单侧检验和双侧检验。单侧检验的界值小于双侧检验的界值,因此更容易拒绝,犯第Ⅰ错误的可能性大。t检验中的p值是接受两均值存在差异这个假设可能犯错的概率。在统计学上,当两组观察对象总体中的确不存在差别时,这个概率与我们拒绝了该假设有关。一些学者认为如果差异具有特定的方向性,我们只要考虑单侧概率分布,将所得到t-检验的P值分为两半。另一些学者则认为无论何种情况下都要报告标准的双侧t检验概率。
3、假设检验的结论不能绝对化。当一个统计量的值落在临界域内,这个统计量是统计上显著的,这时拒绝虚拟假设。当一个统计量的值落在接受域中,这个检验是统计上不显著的,这是不拒绝虚拟假设H0。因为,其不显著结果的原因有可能是样本数量不够拒绝H0
,有可能犯第Ⅰ类错误。
4、正确理解P值与差别有无统计学意义。P越小,不是说明实际差别越大,而是说越有理由拒绝H0
,越有理由说明两者有差异,差别有无统计学意义和有无专业上的实际意义并不完全相同。
5、假设检验和可信区间的关系结论具有一致性差异:提供的信息不同区间估计给出总体均值可能取值范围,但不给出确切的概率值,假设检验可以给出H0成立与否的概率。
6、涉及多组间比较时,慎用t检验。
科研实践中,经常需要进行两组以上比较,或含有多个自变量并控制各个自变量单独效应后的各组间的比较,(如性别、药物类型与剂量),此时,需要用方差分析进行数据分析,方差分析被认为是T检验的推广。在较为复杂的设计时,方差分析具有许多t-检验所不具备的优点。(进行多次的T检验进行比较设计中不同格子均值时)。
编辑本段实际应用
例如,t检验可用于比较男女身高是否存在差别。
为了进行独立样本t检验,需要一个自(分组)变量(如性别:男女)与一个因变量(如测量值)。根据自变量的特定值,比较各组中因变量的均值。用t检验比较下列男、女儿童身高的均值。
1、假设
H0:男平均身高=女平均身高
H1:男身高 不等于 女平均身高
选用双侧检验
选用alpha=0.05的统计显著水平。
2、SPSS中的数据的排列
被试 | 性别 | 身高 |
对象1 对象2 对象3 对象4 对象5 | 男性 男性 男性 女性 女性 | 111 110 109 102 104 |
| | 男性身高均数 = 110 女性身高均数 = 103 | |
3、选择SPSS中compare
means菜单, 独立样本, t-test。选择双侧检验,以及统计显著性水平alpha0.05 。运行。
4、从输出结果查看t检验的p值,是否达到显著水平。是,接受H1。男平均身高与女平均身高不同。否,接受H0,尚无证据支持男女身高差异。
公卫人 附件列表
您所在的用户组无法下载或查看附件
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。

